Il triangolo di Tartaglia (Pascal triangle)

Il triangolo di Tartaglia

Eravamo nel lontano 1983 (ricordo l’uscita dell’ultimo album “The final cut” dei Pink Floyd.), quando frequentai il mio primo corso di informatica.
Era da poco uscito l’avanzatissimo personal computer di Olivetti chiamato M20, ed il corso verteva sulla programmazione in linguaggio Basic in ambito gestionale con sessioni di pratica davanti ad alcuni M20 nuovi fiammanti. In altre parole, un’esperienza da ricordare.

Bé direte voi, cosa centra il Triangolo di Tartaglia?
Fatemi continuare!

Al corso ricevetti una serie di dispense sul Basic (che conservo ancora), e la possibilità di effettuare esperimenti reali su macchina.

Il docente era un giovane da non molto laureato in informatica, dai modi di fare gentili e pacati, che esponeva gli argomenti con molta precisione.
Ci faceva ragionare sulla sintassi del Basic disegnando alla lavagna dei diagrammi che rappresentavano vari percorsi alternativi che alla fine producevano l’espressione da inserire nel programma.

Il primo esercizio di programmazione, fu appunto il calcolo e la stampa del triangolo di Tartaglia.

Si doveva utilizzare una struttura dati chiamata array e riempirla della serie numerica del triangolo che, diciamolo, fornisce, tra le molte altre cose, i coefficienti binomiali dell’espressione algebrica (alla riga n):

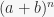
All’epoca del corso non era quindi neanche immaginabile lo sviluppo informatico successivo, ad un corso dove i programmi dovevano essere inseriti ed editati con i numeri di linea, il processore girava a 4 MHz, e l’Hard Disk (quando c’era) poteva superare di poco i 10 MB. Il tutto al costo di ben 16.000.000 di Lire.

Poteva non entrare in Azione Metapost?

L’idea base di Metapost fu resa nota alcuni anni più tardi, nel 1989, e la prima release pubblica risale al 1994.
Questa è un occasione davvero imperdibile: scrivere oggi, con un salto nel tempo, il programma del Triangolo di Tartaglia in Metapost.

L’idea da implementare deve essere, per forza di cose, elegante, almeno per confrontarci con come eravamo allora… (ma anche con il tema del Blog che è “idee nel web”).

   1

  1 1

 1 2 1
 \/
1 3 3 1
...

Un numero nel triangolo si costruisce sommando i due numeri ad esso superiori. Per esempio alla riga quattro, che corrisponde al cubo del binomio, il secondo numero è la somma dei due numeri segnalati dagli slash.

Scartiamo la ricorsione per mantenerci semplici, e valutiamo la seguente idea:
ogni elemento del triangolo si compone di due informazioni: la prima è il valore numerico, la seconda è la coordinata per il posizionamento grafico.

Ogni valore numerico dipende da quelli della riga precedente, ed ad ogni nuova riga troviamo un elemento in più.

Basta dunque lavorare con un array (ancora un array…) chiamato values[], a cui aggiungiamo un elemento alla fine, e lo rielaboriamo tante volte quante sono le righe volute, per trasformarne i valori in quelli corretti di riga.

Abbiamo decritto dunque un classico, due cicli for nidificati, dove nel più interno a partire dalla fine, vengono modificati i valori sommando quelli attuali nell’array (che ancora detengono quelli della riga precedente), e disegnando gli elementi nei punti corretti.

L’informazione della posizione di tracciamento è mantenuta da una variabile punto chiamata pos, che localizza l’ultimo numero sulla riga corrente, mentre la posizione sulla stessa riga è ottenuta sottraendo da pos il vettore (xstep,0) il giusto numero di volte.

Regolando i valori di xstep ed ystep, è possibile aggiustare facilmente l’aspetto del triangolo.

outputtemplate:="tartaglia.mps";

beginfig(1);
   % Tartaglia array values
   numeric values[];
   values[0]=0;

   % triangle deep
   numeric deep;
   deep := 13;

   % position of the triangle top number
   pair pos;
   pos := origin;

   % step among row
   numeric ystep;
   ystep:= 18;
   % step among column
   numeric xstep;
   xstep := 36;

   % main loop
   for k:= 1 upto deep:
      values[k] := 1;
      label("1",pos);

      for i:= k-1 downto 1:
         values[i]:=values[i]+values[i-1];
         label(decimal values[i], pos - (k-i)*(xstep,0));
      endfor;

      pos := pos + (xstep/2,-ystep);
   endfor;
endfig;
end

Il triangolo di Tartaglia

Se avete compreso il codice, e quindi probabilmente l’avete anche eseguito (magari cambiando il numero di righe), e ne siete rimasti colpiti dall’eleganza, allora il merito andrà ad oggi, viceversa, andrà ad un magnifico giorno primaverile di 27 anni fa, quando alla lavagna cominciò a comparire un numero alla volta, il triangolo di Tartaglia.

Ciao, alla prossima.